2  Programming with R

2.1 Tips and strategies

  • When trying to write code to accomplish a particular task—or when trying to understand code written by someone else—try to break the task into individual steps that are accomplished in sequence in order to yield the final result.
  • If you are unsure what a particular bit of code will do—for example, if you want to figure out how to code one of the steps you’ve identified above—try to construct a minimal working example. This example should be simple enough that you can figure out what the result should be without doing any code. Then you can try out the code and verify whether the result matches what you expected.
  • The same principles that underlie producing good code also underlie debugging code. This is covered well in the corresponding chapter of Wickham’s Advanced R book, but essentially debugging involves (a) isolating where the problem arises; (b) understanding the conditions that resulted in the problem; (c) revising the code in an attempt to correct the problem or to prevent problematic circumstances from arising; and (d) testing to ensure the solution in fact addresses the problem. Working on small bits of code at a time makes all of the essential steps of debugging easier.
  • R supports vectorization of many operations. While vectorization allows for code to run more efficiently, the resulting code can sometimes be harder to understand and debug. As a result, you may want to write a less efficient but easier to read version of your code first, so that you can verify that it works the way you expect. You can then see where you might want to try to make your code more efficient, using your original easy-to-read code to verify that any changes you make don’t alter the expected result.
  • Using named vectors/matrices/arrays can often be quite handy when you want to index values by using a string that describes their meaning or interpretation, rather than a numerical index. Not only can this make your code more interpretable, it avoids issues when you may not know ahead of time which numerical index contains a particular desired value.
  • R has a tendency to recycle things in ways you may not expect! For example, when doing any operation involving multiple vectors, if one vector is shorter than the other, R will sometimes “recycle” the elements of the shorter vector to create a new vector that is the same length as the longer one. The rules that govern how R “recycles” are not consistently applied and can be hard to predict, therefore it is important to ensure that your code will not produce this kind of ambiguous situation. You may want to include error checks to ensure that vectors are the same length. Alternatively, if you want to recycle, you can do so explicitly so there is no ambiguity (e.g., x_recycled <- rep(x, length(y))[1:length(y)]).
  • Always remember the drop option when subsetting an array, matrix, or data frame! If the subsetting procedure selects only a single element, unless you use drop = FALSE, the result will be a length-one vector that “throws out” the other dimensions of your data structure. This can result in bugs if your code assumes that the result of the subset will have a consistent number of dimensions.

2.2 Exercise: Fibonnacci

The following set of R coding exercises are meant to prepare you for the kind of coding that will be involved in writing our first cognitive model simulations. It is not exhaustive of all the things that you can do with R, but it addresses many of the essentials. It also exemplifies the workflow involved in building a model:

  1. Implement the basic processes involved in a simple case where you know what the correct result should be, so you can ensure you have implemented these basics appropriately.
  2. Build a function that generalizes the code you wrote in step 1 so that you can apply it to different parameter settings.
  3. Use your function to simulate different results using different parameter settings.
  4. Explore the range of results your function produces across parameter settings.
  5. Optionally, consider ways that you can generalize your model even further by incorporating additional parameters.

These exercises are based on everyone’s favorite sequence, the Fibonnacci sequence. The sequence is defined by a simple rule: the next value in the sequence is the sum of the previous two values. Written in Math, that’s: \[ f[i] = f[i - 2] + f[i - 1] \] where \(f[\cdot]\) is a value in the Fibonnacci sequence and \(i\) is the index of the next value. To get this sequence going, we need to know the first two values, \(f[1]\) and \(f[2]\). Typically, these are both set to 1. As a result, the beginning of the Fibonnacci sequence goes like this: \[ 1, 1, 2, 3, 5, 8, 13, \ldots \]

Anyway, let’s begin!

2.2.1 Exercise 1

Write two versions of a chunk of code that will create a vector called fib that contains the first 20 values in the Fibonnacci sequence. Assume that the first two values in the sequence are 1 and 1. Write one version of the code that creates the vector by appending each new value to the end of fib. Write another version that assigns values to the corresponding entries in fib directly using the appropriate index (for this second version, you may want to use the rep function to create the fib vector).

2.2.2 Exericse 2

Based on the code you wrote for the previous exercise, write a function that returns a vector containing the first N terms of the Fibonnacci sequence. Your function should take two arguments, the value N and a vector called init that contains the first two values in the sequence. Give those arguments sensible default values. The chunk below gives a sense of the overall structure your function should have:

Code 
fib_func <- function(N = ___, init = ___) {
    ...
    return(fib)
}

2.2.3 Exercise 3

Write code that calls the function you wrote in the previous exercise several times, each time using a different value for the second value in the init argument (but the same value for N and for init[1]). Collect the results from each function call in a single data frame or tibble. The data frame or tibble should have a column that stores the second initial value, a column for the vector returned from the function, and a third column that is the value’s index within the sequence. An example of the kind of result you’re looking for is given below:

# A tibble: 8 × 3
  init2   fib     i
  <dbl> <dbl> <int>
1     1     1     1
2     1     1     2
3     1     2     3
4     1     3     4
5     4     1     1
6     4     4     2
7     4     5     3
8     4     9     4

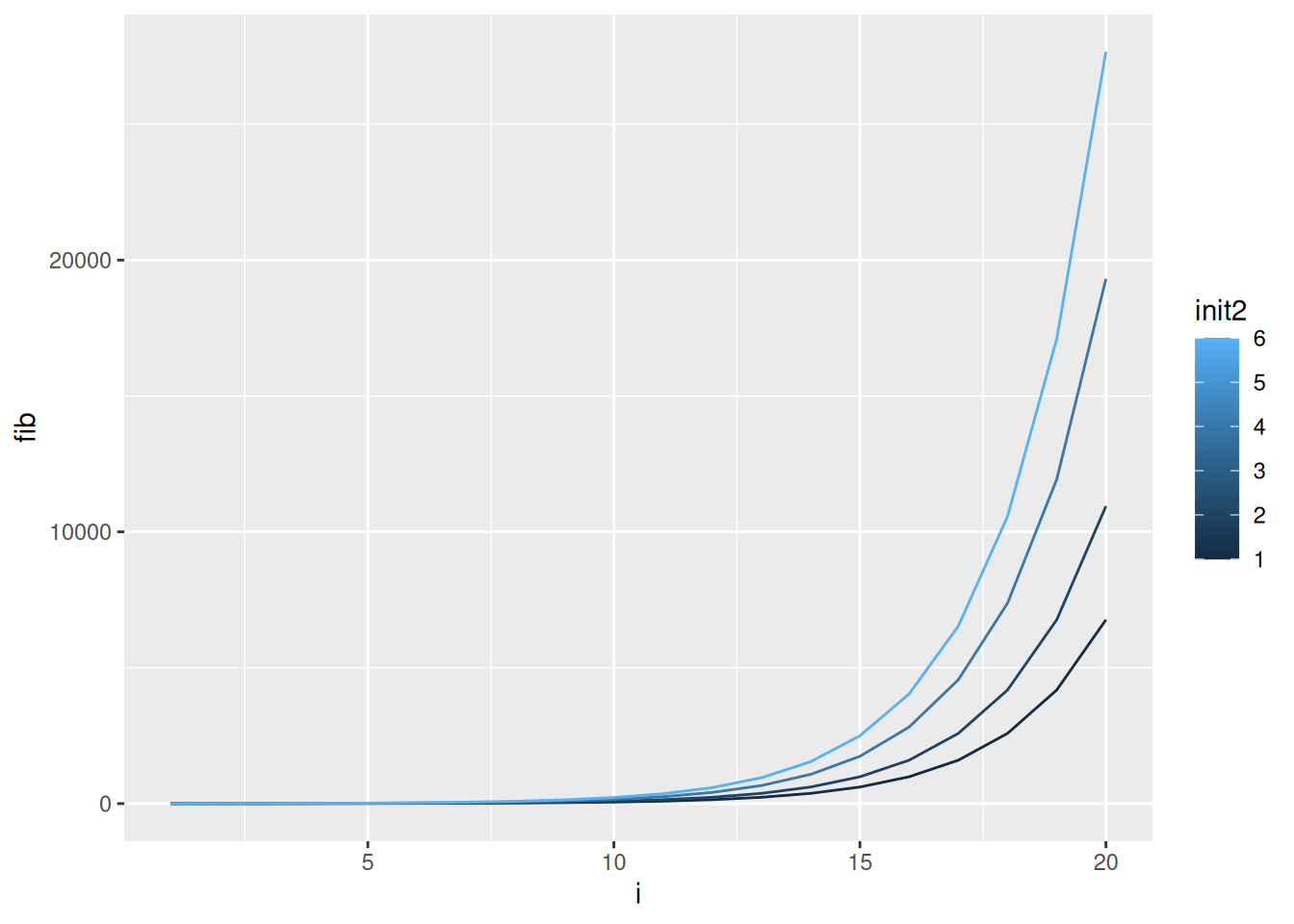
2.2.4 Exercise 4

Write code that uses the ggplot2 library to plot the values of the Fibonnacci sequence on the y-axis against their position in the sequence on the x-axis. Distinguish between different init2 values by using different colored lines. The result should look something like the plot below.

2.2.5 Extension exercise

Write a new function that takes a third argument, n_back, which specifies how many of the previous values to add up to create the next value in the sequence. For the Fibonnacci sequence, n_back = 2, but in principle we could define other kinds of sequences too. Adapt the code you wrote for your previous exercises to explore what happens with different values of n_back. You may also want to include some code at the beginning of your function that checks to ensure that the number of initial values provided in the init argument is sufficient!